TYT Geometri sınavında üçgenler, en çok soru çıkan ve en fazla puan kazandıran konuların başında gelir. Öğrencilerin karşılaştığı en büyük sorun, çok sayıda formül ve kuralın birbirine karışması ve sınav anında hangisini kullanacaklarını bilememeleridir. Bu yazıda, üçgenlerle ilgili bilmeniz gereken 12 temel kuralı tek sayfada, net ve uygulanabilir şekilde bulacaksınız.
Bu kuralları öğrendikten sonra, TYT'de karşınıza çıkacak üçgen sorularının büyük bölümünü rahatlıkla çözebileceksiniz. Her kural, gerçek sınav mantığıyla örneklendirilmiş ve pratik uygulamaya hazır hale getirilmiştir.
Özel Ders Alanı
En İyi Geometri Öğretmenlerinden Ders Al
6-8
TYT'de Ortalama Geometri Sorusu
40%
Geometri Sorularında Üçgen Oranı
12
Mutlaka Bilinmesi Gereken Kural
"Bu 12 kuralı ezberlemek yerine anlamak, TYT Geometri başarınızı iki katına çıkarabilir."
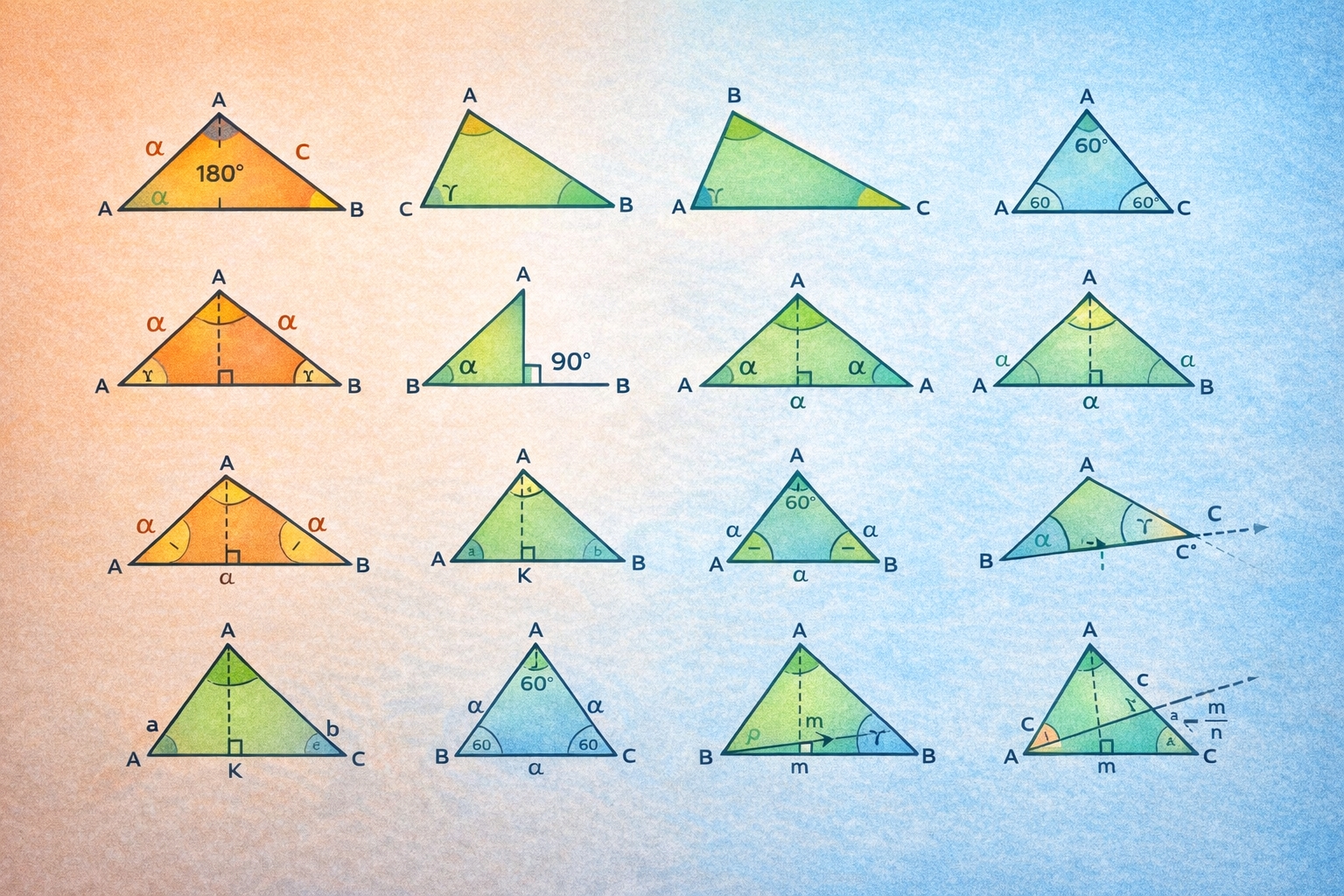
Açılar Toplamı Kuralı
Her üçgende iç açılar toplamı her zaman 180 derecedir. Bu en temel kural olmakla birlikte, TYT'de en sık kullanılan kuraldır.
Pratik kullanım: İki açısı verilmiş bir üçgende üçüncü açıyı bulmak için diğer iki açıyı toplayıp 180'den çıkarın.
Örnek Soru
Bir üçgenin iki açısı 45° ve 65° ise, üçüncü açısı kaç derecedir?
Çözüm: 180° - (45° + 65°) = 180° - 110° = 70°
Dış Açı Kuralı
Üçgenin bir dış açısı, kendisine komşu olmayan iki iç açının toplamına eşittir. Bu kural, TYT'de açı hesaplamalarını hızlandırır.
Sınav ipucu: Dış açı sorularında önce komşu olmayan iç açıları belirleyin, sonra toplayın. 180'den çıkarmaya gerek yoktur.
Kenar-Açı İlişkisi
Üçgende en büyük açının karşısındaki kenar en uzundur, en küçük açının karşısındaki kenar en kısadır. Bu ilişki her zaman geçerlidir.
TYT'de bu kural, özellikle kenar uzunlukları karşılaştırma sorularında kullanılır. Açıları karşılaştırarak kenarlar hakkında doğrudan sonuç çıkarabilirsiniz.
Üçgen Eşitsizliği
Bir üçgende herhangi iki kenarın toplamı, üçüncü kenardan büyüktür. Ayrıca, herhangi iki kenarın farkı, üçüncü kenardan küçüktür.
Bu kural, bir üçgenin var olup olamayacağını test etmek için kullanılır. Matematik derslerinde bu ilişki sıklıkla sorgulanır.
Pratik Uygulama
5 cm ve 8 cm kenarları olan bir üçgenin üçüncü kenarı hangi aralıkta olabilir?
Çözüm: 8 - 5 < x < 8 + 5 → 3 < x < 13
İkizkenar Üçgen Özellikleri
İkizkenar üçgende eşit kenarların karşısındaki açılar eşittir. Ayrıca, tepe açısının açıortayı aynı zamanda tabanı ortalar ve tabana diktir.
TYT'de ikizkenar üçgen sorularında bu özellikler sıklıkla birlikte kullanılır. Bir özellik verildiğinde diğerlerini otomatik olarak uygulayabilirsiniz.
Eşkenar Üçgen Formülleri
Eşkenar üçgende tüm açılar 60 derecedir ve tüm kenarlar eşittir. Kenar uzunluğu a olan eşkenar üçgenin yüksekliği (a√3)/2, alanı ise (a²√3)/4'tür.
Bu formüller ezber gibi görünse de mantığını anlamak önemlidir. İstanbul matematik özel ders hizmetlerinde bu konu detaylıca işlenir.
Yükseklik
Kenar uzunluğu: a
h = (a√3)/2
Alan
Kenar uzunluğu: a
A = (a²√3)/4
Dik Üçgen ve Pisagor Teoremi
Dik üçgende hipotenüsün karesi, dik kenarların karelerinin toplamına eşittir: a² + b² = c². Bu, geometri konularının en temel ve en çok kullanılan formülüdür.
TYT'de özel üçgenler olan 3-4-5, 5-12-13 ve 8-15-17 üçlülerini ezbere bilmek zaman kazandırır.
| Dik Kenar 1 | Dik Kenar 2 | Hipotenüs |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 8 | 15 | 17 |
| 6 | 8 | 10 |
30-60-90 Özel Üçgeni
30-60-90 üçgeninde kenarlar 1 : √3 : 2 oranındadır. 30 derecenin karşısı en kısa kenar, 60 derecenin karşısı orta kenar, 90 derecenin karşısı hipotenüstür.
Bu oran TYT'de çok sık kullanılır. Özellikle eşkenar üçgenin yarısı alındığında ortaya çıkar.
45-45-90 Özel Üçgeni
45-45-90 üçgeninde kenarlar 1 : 1 : √2 oranındadır. Bu üçgen aynı zamanda ikizkenar dik üçgendir.
Kare köşegenle ikiye bölündüğünde 45-45-90 üçgenleri oluşur. Bu özellik TYT'de kare ve üçgen birlikte sorulduğunda kullanılır.
30-60-90
Kenar Oranları
1 : √3 : 2
45-45-90
Kenar Oranları
1 : 1 : √2
Kenarortay Teoremi
Kenarortay, bir köşeden karşı kenarın ortasına çizilen doğrudur. Üçgende üç kenarortay ağırlık merkezinde kesişir ve ağırlık merkezi her kenarortayı 2:1 oranında böler.
TYT'de kenarortay soruları genellikle ağırlık merkezi ve oran kavramlarını birlikte kullanır. İzmir matematik özel dersi alan öğrenciler bu konuda sıklıkla pratik yaparlar.
Açıortay Teoremi
Açıortay, bir açıyı iki eşit parçaya bölen doğrudur. Açıortay karşı kenarı, köşeye bitişik kenarlarla orantılı olarak böler.
Matematiksel ifade: Eğer AD açıortaysa ve AB = m, AC = n ise, BD/DC = m/n olur. Bu oran ilişkisi TYT'de sık sorulur.
Alan Formülleri
Üçgen alanı hesaplamak için birkaç farklı yöntem vardır. En temel formül: Alan = (taban × yükseklik) / 2. Ayrıca, üç kenarı bilinen üçgenlerde Heron formülü kullanılır.
Heron formülü: Alan = √[u(u-a)(u-b)(u-c)] burada u = (a+b+c)/2 çevrenin yarısıdır. Bu formül kenar uzunlukları verildiğinde pratiktir.
Temel Formül
Taban ve Yükseklik
A = (t × h) / 2
Heron Formülü
Üç Kenar Biliniyor
A = √[u(u-a)(u-b)(u-c)]
Trigonometrik
İki Kenar ve Aralarındaki Açı
A = (a × b × sinC) / 2
TYT'de Zaman Kazandıran Pratik İpuçları
Şekil Üzerinde İşaretleme
Verilen bilgileri mutlaka şekil üzerine yazın. Eşit açıları, eşit kenarları işaretleyin. Bu görsel hafızanızı güçlendirir ve hatayı azaltır.
Özel Üçgenleri Tanıyın
3-4-5, 5-12-13, 30-60-90 ve 45-45-90 üçgenlerini hemen fark edin. Bu üçgenlerde uzun hesaplara girmeden doğrudan oranları kullanabilirsiniz.
Yardımcı Çizgiler Atın
Bazen bir yükseklik, kenarortay veya açıortay çizmek soruyu çok kolaylaştırır. Özellikle ikizkenar ve eşkenar üçgenlerde bu strateji işe yarar.
Açı-Kenar Eşitliklerini Kontrol Edin
İki açı eşitse karşısındaki kenarlar eşittir, iki kenar eşitse karşısındaki açılar eşittir. Bu basit ilişki birçok sorunun anahtarıdır.
TYT'de Sık Yapılan Hatalar
Açı ve Kenar Karıştırma
En büyük açının karşısında en büyük kenar vardır denmesi gerekirken, tam tersi söylenir. Bu ilişkiyi her zaman doğru hatırlayın.
Pisagor Teoremini Yanlış Uygulamak
Pisagor teoremi sadece dik üçgenlerde geçerlidir. Başka üçgenlerde kullanırsanız sonuç yanlış çıkar. Önce üçgenin dik olup olmadığını kontrol edin.
Alan Formülünde Birimi Unutmak
Alan her zaman kare birim cinsinden verilir. Kenar uzunluğu cm ise alan cm², metre ise m² olmalıdır. Birim dönüşümlerine dikkat edin.
Önemli
Bu 12 kuralı ezberlemek yerine anlamaya ve uygulamaya odaklanın. Her kuralın mantığını kavradığınızda, TYT'de karşınıza çıkabilecek tüm üçgen sorularını rahatlıkla çözebilirsiniz. Düzenli pratik yapmayı unutmayın.
30 Günlük Üçgenler Çalışma Planı
| Gün | Konu | Soru Sayısı |
|---|---|---|
| 1-3 | Açılar Toplamı ve Dış Açı | 20 soru/gün |
| 4-6 | Kenar-Açı İlişkisi ve Üçgen Eşitsizliği | 25 soru/gün |
| 7-10 | İkizkenar ve Eşkenar Üçgenler | 30 soru/gün |
| 11-15 | Dik Üçgen ve Pisagor | 35 soru/gün |
| 16-20 | Özel Üçgenler (30-60-90 ve 45-45-90) | 30 soru/gün |
| 21-25 | Kenarortay, Açıortay ve Alan | 35 soru/gün |
| 26-30 | Karma Sorular ve Deneme | 40 soru/gün |
Sonuç ve Öneriler
TYT Geometri başarısının anahtarı, bu 12 temel kuralı ezbere değil anlayarak öğrenmektir. Her kural birbirleriyle bağlantılıdır ve gerçek sınav sorularında genellikle birden fazla kural birlikte kullanılır.
Düzenli pratik yapmak, bu kuralları içselleştirmenin en etkili yoludur. Günde en az 20-30 üçgen sorusu çözerek bu konuda ustalaşabilirsiniz. Özellikle özel üçgenleri (3-4-5, 30-60-90, 45-45-90) tanımak, sınav sırasında size büyük zaman kazandırır.
Unutmayın ki geometri görsel bir konudur. Şekil çizme ve üzerinde işaretleme alışkanlığı kazanmak, hem anlama hem de doğru çözüm bulma konusunda size yardımcı olacaktır. Başarılar dileriz.
Son Tavsiye
Konuyu kavradıktan sonra mutlaka karma sorular ve deneme sınavları çözün. Gerçek TYT sorularının mantığını anlamak, sadece kural bilmekten daha önemlidir. Zorlandığınız noktalarda profesyonel destek almaktan çekinmeyin.
TYT Geometride Başarıya Hazır mısınız?
Bu 12 kuralı içselleştirin, düzenli pratik yapın ve hedeflerinize ulaşın. Başarı sistematik çalışmanın sonucudur.









Görüşlerinizi Bizimle Paylaşın (0)